Bạn có biết các nhà toán học làm cách nào để miêu tả pi trước khi từ pi ra đời? Chúng ta có thể tính p bằng phương trình đại số hay không? Số Pi liên quan đến công trình nổi tiếng nào ở Ai Cập huyền bí? Cùng MATHX đi tìm hiểu chi tiết qua bài viết bên dưới nhé
Ký hiệu Pi (π)
Ký hiệu pi (π) có từ lúc nào? Trước khi có ký hiệu pi, các nhà toán học phải dùng khá nhiều từ "đại lượng mà khi nhân nó với đường kính sẽ được chu vi". Tên pi ngày nay là sáng tạo của một nhà toán học ít tên tuổi xứ Wales William Jones (1675 - 1749), bạn thân của Isaac Newton. Jones là người ký hiệu π với công chúng vào năm 1706 nhưng người làm cho ký hiệu π trở nên phổ biến là Leonhard Euler. Cùng với Newton và Archimedes, Leonhard Euler là một trong những nhà toán học vĩ đại nhất mọi thời đại và là nhà toán học xuất sắc nhất thế kỷ 18. Euler đã có rất nhiều khám phá quan trọng và có ảnh hưởng lớn trong các bộ môn toán như vi tích phân, lý thuyết số giải tích. Euler cũng là người giới thiệu nhiều khái niệm và ký hiệu toán học hiện đại như hàm số toán học trong giải tích.
Chữ cái Hy Lạp
π là chữ cái đầu tiên của các từ periphery và perimeter trong tiếng Anh (đều có nghĩa là chu vi, cũng như circumference). Và như tất cả chúng ta đã biết, pi là tỉ số giữa chu vi của đường tròn với đường kính của nó.
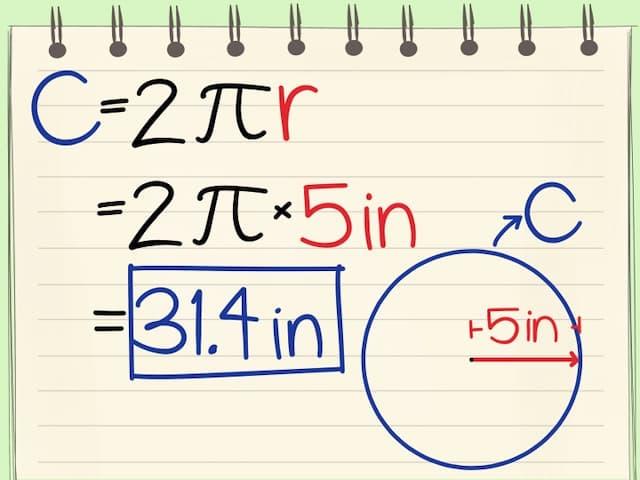
Nếu bạn không phải là người đam mê toán, bạn sẽ ngạc nhiên khi biết rằng chúng ta không thể tìm được giá trị chính xác của pi.
Trong toán học, pi là một số "siêu việt". Cuối thế kỷ 18, hai nhà toán học Johann Heinrich Lambert (1728-1777) và Adrien-Marie Legendre (1752-1833) đã chứng minh được rằng pi là số vô tỉ vì không thể tính được tan của pi bằng phân số liên tục (còn gọi là liên phân số-continued fraction), đồng nghĩa với việc không thể tính pi bằng phân số.
Liên phân số là một công cụ toán học hữu hiệu được các nhà toán học sử dụng để giải nhiều bài toán khó. Liên phân số có dạng một phân số nhiều tầng như hình dưới.
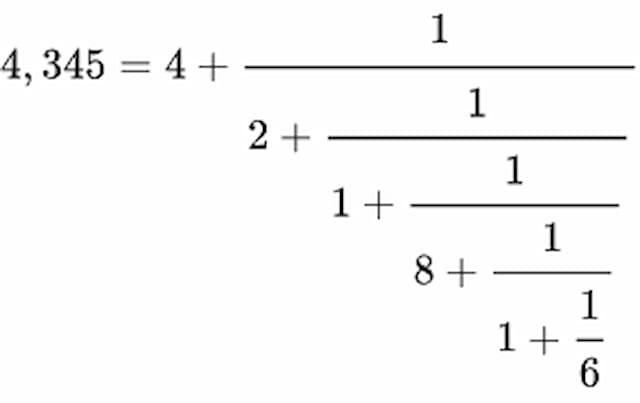
trong đó b0 là số nguyên không âm và tất cả b đều nguyên dương.
Vì pi là một số vô tỉ, không thể biểu diễn dưới dạng phân số của các số nguyên nên việc khám phá pi càng thú vị hơn với các nhà toán học. Họ có thể biểu diễn con số thần thánh này dưới các hình thức khác: các dãy số và thuật toán.
Vì chúng ta không bao giờ có thể tính được giá trị chính xác của pi nên chúng ta cũng không bao giờ có thể tìm được diện tích hay chu vi chính xác của một đường tròn.
Nhiều nhà toán học tin rằng, sẽ là chính xác hơn khi nói rằng, một đường tròn có số góc là vô hạn so với việc nói đường tròn không có góc nào. Chỉ có một lý do hợp lý duy nhất: số góc "vô hạn" này tương quan với số chữ số vô hạn của pi.
Có nhiều bằng chứng cho thấy pi đã được khám phá cách đây rất lâu. Cách đây 4.000 năm, người Babylon ở thời văn minh Lưỡng Hà (Mesopotamia) đã biết đến pi và có bằng chứng cho thấy họ tính được pi là 3,125.
Số pi cũng có mặt trong King James Bible, bản Kinh Thánh bằng tiếng Anh xuất bản năm 1611 dưới sự tài trợ của vua Anh James I. Cuốn sách này đưa ra một giá trị Pi gần đúng là bằng 3. Đơn vị tính pi thời đó là cubit, một đơn vị đo lường cổ. 3 cubits tương đương 45,72 cm ngày nay (18 inch), bằng khoảng cách từ cùi chỏ tới đầu ngón tay giữa.
>>> Tham khảo thêm: NHỮNG ĐIỀU KHÓ KHĂN VỀ SỐ PI
Sự hữu ích của pi là một vấn đề tranh cãi mặc dù nó được nhiều người yêu toán quý mến. Một số cho rằng, số tau (có giá trị bằng 2π) là một số vô tỉ có tính trực giác và phù hợp hơn. Ví dụ, bạn có thể nhân tau với bán kính và tính chu vi của một đường tròn chỉ qua quan sát trực tiếp mà không cần suy nghĩ. Tau/4 cũng đại diện cho một góc tư đường tròn. Vì vậy, tính trực giác của tau khiến nó hấp dẫn hơn trong mắt một số người yêu toán.
Pi là một phần của thần thoại Ai Cập. Người dân Ai Cập tin rằng các kim tự tháp Giza được xây dựng theo các nguyên tắc của pi. Chiều cao của các kim tự tháp có mối quan hệ giống với chu vi của đáy kim tự tháp, giống như quan hệ giữa bán kính và chu vi của đường tròn. Bên trong kim tự tháp Giza là những cấu trúc lạ lùng và Giza là kỳ quan duy nhất trong bảy kỳ quan của thế giới cổ đại còn tồn tại đến hôm nay, thu hút vô số du khách. Việc xem π là nguyên tắc chính khiến pi trở thành một con số đặc biệt đối với các kiến trúc sư.
Việc sử dụng số Pi đã tiến hóa theo thời gian
Trước thế kỷ 17, pi chỉ được dùng trong các bài toán về đường tròn, như đã đề cập ở trên về mối quan hệ giữa pi và đường tròn.
Đến thế kỷ 17, người ta nhận ra rằng pi cũng có thể được dùng để tính diện tích, chu vi của các đường cong khác như chiều dài cung tròn (arc), hypocycloid (đường cong được tạo thành bởi một điểm cố định trong một đường tròn nhỏ khi đường tròn nhỏ đó quay tròn bên trong một đường tròn khác có bán kính lớn hơn nó nhiều lần). Và đến thế kỷ 20, pi được dùng trong nhiều ứng dụng đa dạng các lĩnh vực như xác suất, các lý thuyết toán học khác.
Pi còn được dùng để tính chu vi trái đất. Tuy việc tính toán giá trị của pi khá khó khăn nhưng pi là một con số siêu hiệu quả trong các phép tính cần đến nó. Ví dụ, nếu bạn làm tròn số pi lên tới 9 chữ số sau dấu thập phân và dùng nó để tính chu vi trái đất, bạn sẽ thu được những kết quả rất chính xác. Với mỗi 40.000 km, số pi chỉ sai khoảng 0,62 cm (¼ inch). Nếu bạn yêu toán, bạn sẽ nhận ra điều này thật sự tuyệt vời như thế nào.


