Xem tài liệu

Ví dụ 1: Cho hai hàm số $f(x)=dfrac{(m-1)x-2m}{x-2}$ và $g(x)={{2}^{-ln (x+1)}}+dfrac{1}{{{2}^{x}}-1}+dfrac{x+1}{x-3}.$ Đồ thị của hai hàm số đã cho cắt nhau tại đúng hai điểm có hoành độ dương khi và chỉ khi

A. $min left( 2;+infty right).$

B. $min left( 0;2 right).$

C. $min left[ 2;+infty right).$

D. [min left( -infty ;2 right].]

Link câu hỏi: https://www.askmath.vn/cau-hoi/cho-hai-ham-so-va-do-thi-cua-hai-ham-so-da-cho-cat-nhau-tai-dung/7e9b7b15-c255-4d06-94e5-88168766de52

Phương trình hoành độ giao điểm: ${{2}^{-ln (x+1)}}+dfrac{1}{{{2}^{x}}-1}+dfrac{x+1}{x-3}=dfrac{(m-1)x-2m}{x-2}=m-dfrac{x}{x-2}Leftrightarrow m=h(x)={{2}^{-ln (x+1)}}+dfrac{1}{{{2}^{x}}-1}+dfrac{x+1}{x-3}+dfrac{x}{x-2}(*).$

Xét hàm số $h(x)={{2}^{-ln (x+1)}}+dfrac{1}{{{2}^{x}}-1}+dfrac{x+1}{x-3}+dfrac{x}{x-2}$ trên $D=left( 0;+infty right)backslash {2,3}.$

Có ${h}'(x)=-dfrac{1}{x+1}{{2}^{-ln (x+1)}}ln 2-dfrac{{{2}^{x}}ln 2}{{{left( {{2}^{x}}-1 right)}^{2}}}-dfrac{4}{{{left( x-3 right)}^{2}}}-dfrac{2}{{{left( x-2 right)}^{2}}}<0,forall xin D.$

Bảng biến thiên:

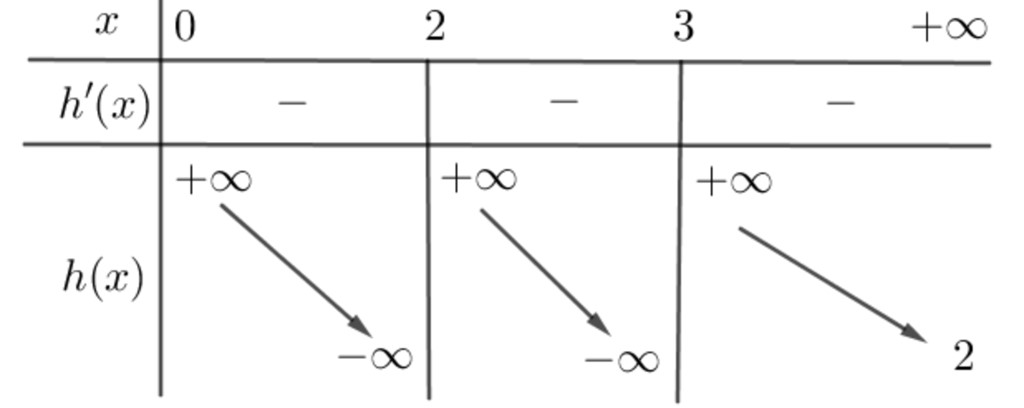
Vậy cắt tại đúng hai điểm có hoành độ dương khi và chỉ khi (*) có đúng hai nghiệm dương. Quan sát bảng biến thiên suy ra $mle 2.$ Chọn đáp án D.

Ví dụ 2: Cho hai hàm số $y=ln left| dfrac{x-2}{x} right|$ và $y=dfrac{3}{x-2}-dfrac{1}{x}+4m-2020.$ Tổng tất cả các giá trị nguyên của tham số $m$ để đồ thị của hai hàm số đã cho cắt nhau tại một điểm duy nhất bằng

A. $506.$

B. $1011.$

C. $2020.$

D. $1010.$

Link câu hỏi: https://www.askmath.vn/cau-hoi/cho-hai-ham-so-yln-left-dfracx2x-right-va/4d0dd203-e801-4638-a2b3-f118baa04a2c

Phương trình hoành độ giao điểm. $ln left| dfrac{x-2}{x} right|=dfrac{3}{x-2}-dfrac{1}{x}+4m-2020Leftrightarrow m=g(x)=dfrac{1}{4}left[ ln left| dfrac{x-2}{x} right|-dfrac{3}{x-2}+dfrac{1}{x}+2020 right].$

Điều kiện. $xin mathbb{R}backslash {0,2}.$ Có ${g}'(x)=dfrac{1}{4}left( dfrac{2}{x(x-2)}+dfrac{3}{{{(x-2)}^{2}}}-dfrac{1}{{{x}^{2}}} right)=0Leftrightarrow x=pm 1.$

Bảng biến thiên:Cắt nhau tại 1 điểm khi và chỉ khi (*) có đúng 1 nghiệm. Từ bảng biến thiên suy ra $m=505;m=506;m=505+dfrac{ln 3}{4}.$ Tổng các số nguyên cần tìm bằng $505+506=1011.$ Chọn đáp án B.

Ví dụ 3: Cho hai hàm số $y=left( x+1 right)left( 2x+1 right)left( 3x+1 right)left( m+left| 2x right| right);y=-12{{x}^{4}}-22{{x}^{3}}-{{x}^{2}}+10x+3$ có đồ thị lần lượt là $({{C}_{1}}),({{C}_{2}}).$ Có bao nhiêu giá trị nguyên của tham số [m] trên đoạn [left[ -2020;2020 right]] để $({{C}_{1}})$ cắt $({{C}_{2}})$ tại 3 điểm phân biệt?

A. [4040.]

B. [2020.]

C. [2021.]

D. [4041.]

Giải. Phương trình hoành độ giao điểm:

$begin{gathered} left( {x + 1} right)left( {2x + 1} right)left( {3x + 1} right)left( {m + left| {2x} right|} right) = - 12{x^4} - 22{x^3} - {x^2} + 10x + 3 hfill Leftrightarrow m + left| {2x} right| = dfrac{{ - 12{x^4} - 22{x^3} - {x^2} + 10x + 3}}{{left( {x + 1} right)left( {2x + 1} right)left( {3x + 1} right)}} = - 2x + dfrac{1}{{x + 1}} + dfrac{1}{{2x + 1}} + dfrac{1}{{3x + 1}} hfill Leftrightarrow m = g(x) = - 2left( {x + left| x right|} right) + dfrac{1}{{x + 1}} + dfrac{1}{{2x + 1}} + dfrac{1}{{3x + 1}}(*). hfill end{gathered} $

*Chú ý: $dfrac{-12{{x}^{4}}-22{{x}^{3}}-{{x}^{2}}+10x+3}{left( x+1 right)left( 2x+1 right)left( 3x+1 right)}=-2x+dfrac{1}{x+1}+dfrac{1}{2x+1}+dfrac{1}{3x+1}$ phân tích tương tự phương pháp tìm nguyên hàm hàm phân thức hữu tỷ.

Có ${g}'(x)=-2left( 1+dfrac{x}{left| x right|} right)-dfrac{1}{{{left( x+1 right)}^{2}}}-dfrac{2}{{{left( 2x+1 right)}^{2}}}-dfrac{3}{{{left( 3x+1 right)}^{2}}}<0,forall xin mathbb{R}backslash left{ 0,-1,-dfrac{1}{2},-dfrac{1}{3} right}.$

Bảng biến thiên:

Vậy $({{C}_{1}})$ cắt $({{C}_{2}})$ tại 3 điểm phân biệt khi và chỉ khi (*) có ba nghiệm phân biệt$Leftrightarrow mge 0Rightarrow min left{ 0,...,2020 right}.$ Chọn đáp án C.

Ví dụ 4: Có bao nhiêu $m$ nguyên dương để hai đường cong $({{C}_{1}}):y=left| 2+dfrac{2}{x-10} right|$ và $({{C}_{2}}):y=sqrt{4x-m}$ cắt nhau tại ba điểm phân biệt có hoành độ dương?

A. $35.$

B. $37.$

C. $36.$

D. $34.$

Phương trình hoành độ giao điểm:

$sqrt{4x-m}=left| 2+dfrac{2}{x-10} right|Leftrightarrow 4x-m={{left( 2+dfrac{2}{x-10} right)}^{2}}Leftrightarrow m=g(x)=4x-{{left( 2+dfrac{2}{x-10} right)}^{2}}(*).$

Ta cần tìm $m$ để (*) có đúng ba nghiệm dương.

Xét hàm số [g(x)=4x-{{left( 2+dfrac{2}{x-10} right)}^{2}}] trên $left( 0;+infty right)backslash {10}$ có

${g}'(x)=4-2left( 2+dfrac{2}{x-10} right)left( -dfrac{2}{{{(x-10)}^{2}}} right)=0overset{0<xne 0}{longleftrightarrow}x={{x}_{0}}approx 9,2291.$

Bảng biến thiên:

Quan sát bảng biến thiên suy ra $-dfrac{81}{25}<m<36,563Rightarrow min left{ 1,...,36 right}$ có 36 số nguyên dương thoả mãn. Chọn đáp án C.